Bitcoin White Paper – Norsk Versjon
Les den norske versjonen av Bitcoin sitt opprinnelige white paper. Oversatt av Torbjørn Bull Jenssen og Sander Westnes.


Dokumentet var på den tid allerede oversatt til 23 språk, og det føltes derfor naturlig å lage en versjon på norsk. Den norske utgaven er nå lastet opp til bitcoin.org.
Her finner du en komplett tekstoversettelse av innholdet, inkludert en PDF versjon. Matematiske uttrykk og beregninger er omformet til bidelfiler. Siste del inneholder en kommentar fra oversetter.
Bitcoin: Et peer-to-peer elektronisk kontantsystem
Satoshi Nakamoto [email protected]
www.bitcoin.org
Translated into Norwegian Bokmål from bitcoin.org/bitcoin.pdf by kryptografen.no
Sammendrag: En fullstendig «peer-to-peer»-versjon av et elektronisk kontantsystem vil muliggjøre direktebetalinger på nett fra en part til en annen uten å måtte gå gjennom en finansiell institusjon. Digitale signaturer utgjør en del av løsningen, men de største fordelene går tapt hvis en betrodd tredjepart fortsatt er nødvendig for å unngå dobbeltbruk. Vi foreslår en løsning på dobbeltbruksproblemet ved å bruke et P2P-nettverk.
Nettverket tidsstempler transaksjoner gjennom hashberegninger i en løpende kjede av hash-basert proof-of-work, noe som skaper en historikk som ikke kan endres uten at proof-of-work-arbeidet må gjøres på nytt.
Den lengste kjeden fungerer ikke bare som et bevis på rekkefølgen av hendelser som har funnet sted, men som et bevis på at den kom fra den største samlingen av CPU-kraft. Så lenge brorparten av CPU-kraften er kontrollert av noder som ikke samarbeider for å angripe nettverket, vil de generere den lengste kjeden og utkonkurrere eventuelle angripere. Nettverket krever i seg selv minimalt med struktur. Meldinger sendes ut etter beste evne, og noder kan forlate og koble seg til nettverket som de selv vil, og akseptere den lengste proof-of-work-kjeden som bevis på hva som skjedde mens de var borte.
1. Introduksjon
Handel på Internett er blitt så godt som totalt avhengig av tjenester fra finansielle institusjoner, som fungerer som en betrodd tredjepart ved elektronisk betaling. Selv om systemet fungerer godt nok for de fleste transaksjoner, lider det fortsatt av de innebygde svakhetene i den tillitbaserte modellen. Fullstendig irreversible transaksjoner er umulig, siden finansielle institusjoner ikke kan unngå å måtte håndtere tvister.
Kostnadene ved mekling øker transaksjonskostnadene, begrenser den minimale praktiske transaksjonsstørrelsen og reduserer muligheten for små uformelle transaksjoner, og det er en større kostnad ved at man ikke har mulighet til å foreta irreversible betalinger for irreversible tjenester. Med muligheten for reversering øker behovet for tillit. Selgere må være varsomme med sine kunder, og kreve mer informasjon fra dem enn hva som ellers ville vært nødvendig. En viss prosent svindel aksepteres som uunngåelig. Disse kostnadene og usikkerhetene ved betaling kan unngås ved å betale med fysisk valuta, men ingen mekanisme eksisterer for å utføre betalinger over en kommunikasjonskanal uten en betrodd part.
Det som behøves er et elektronisk betalingssystem basert på kryptografiske bevis i stedet for tillit, noe som lar to villige parter samhandle direkte, uten behov for en betrodd tredjepart. Transaksjoner som er beregningsmessig upraktiske å reversere, ville beskyttet selgere mot svindel, og rutinemessige deponerings-mekanismer kan enkelt implementeres for å beskytte kjøpere.
I denne artikkelen foreslår vi en løsning mot problemet med dobbeltbruk som anvender en peer-to- peer, distribuert tidsstemplingsserver for å generere beregningsmessige bevis for den kronologisk rekkefølgen på transaksjonene. Systemet er trygt så lenge pålitelige noder har kontroll over mer CPU-kraft enn enhver annen samarbeidende gruppe med angripende noder.
2. Transaksjoner
Vi definerer en elektronisk mynt som en kjede av digitale signaturer. Hver eier overfører mynten til neste eier ved å digitalt signere den foregående transaksjonens hashverdi samt neste eiers offentlige nøkkel og legge disse til på slutten av mynten. En betalingsmottaker kan verifisere signaturer for å validere kjeden av eiere.
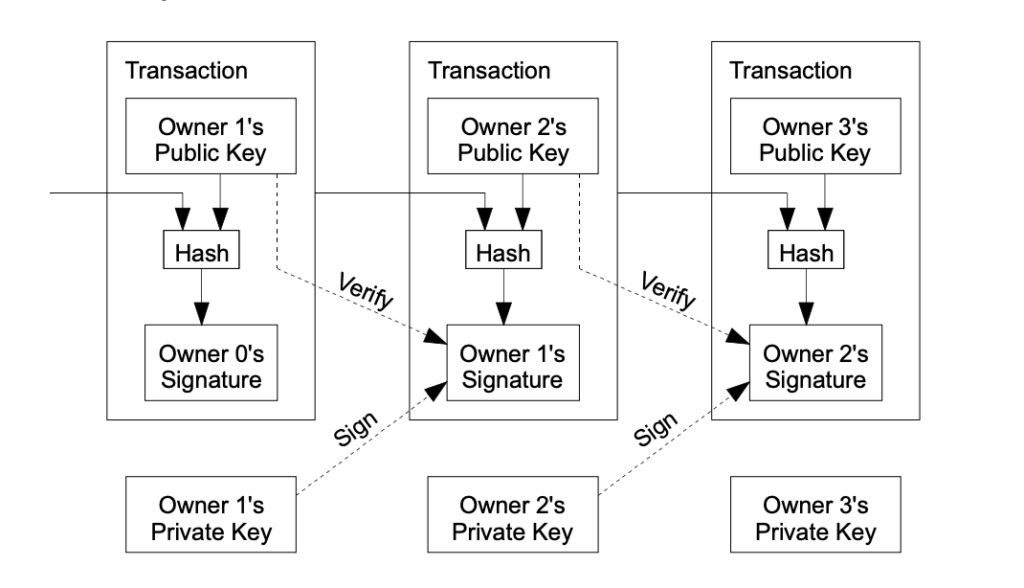
Problemet er selvfølgelig at betalingsmottakeren ikke kan sjekke om noen av de tidligere eierne har dobbeltbrukt mynten. En vanlig løsning er å introdusere en betrodd sentral autoritet, eller «et myntverk», som sjekker hver transaksjon for dobbeltbruk. Etter hver transaksjon, må mynten returneres til utgiveren som får utgi en ny mynt, og bare mynter utgitt direkte fra utgiveren/myntverket kan man stole på at ikke er blitt dobbeltbrukt. Problemet med denne løsningen er at skjebnen til hele pengesystemet er avhengig av myntverket, siden hver transaksjon må gå gjennom dem, akkurat som med en bank.
Vi trenger en løsning slik at betalingsmottakeren kan vite med sikkerhet at de tidligere eierne ikke har signert noen andre transaksjoner tidligere. For vårt formål er det den første transaksjonen som teller, så vi bryr oss ikke om senere forsøk på dobbeltbruk. Den eneste måten å bekrefte fraværet av en transaksjon, er å ha oversikt over alle transaksjoner. I myntmodellen med en sentral utgiver, har utgiveren oversikt over alle transaksjoner og avgjør hvilke som ankommer først. For å oppnå dette uten et betrodd mellomledd, må transaksjoner bli offentligjort [1], og vi trenger et system slik at deltakere kan bli enige om en historikk over rekkefølgen de ble mottatt i. Betalingsmottakeren behøver bevis på at, for enhver transaksjon, er majoriteten av nodene er enige om at transaksjonen var den første.
3. Tidsstemplingsserver
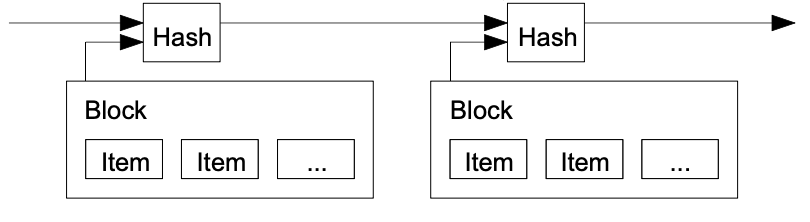
Løsningen vi foreslår begynner med en tidsstemplingsserver. En tidsstemplingsserver fungerer ved å først beregne hashverdien av en blokk med enheter som skal tidsstemples og så offentliggjøre resultatet gjennom bred publisering, som i en avis eller et Usenet-innlegg [2-5]. Tidsstempelet beviser at dataene må ha eksistert på tidspunktet, noe som åpenbart er nødvendig for å at dataene kan ha blitt inkludert i hashberegningen. Hvert tidsstempel inkluderer det forrige tidsstempelet i hashberegningen, hvor hvert ekstra tidsstempel forsterker de foregående.
4. Proof-of-Work
For å implementere en distribuert tidsstemplingsserver i et P2P-nettverk, behøver vi å bruke en proof-of-work metode liknende Adam Backs Hashcash [6], i stedet for en avis eller et Usenet- innlegg. Proof-of-work, bevis på utført arbeid, innebærer å søke etter en verdi som ved en hashberegning, som for eksempel SHA-256, gjør at blokkens hashverdi starter med et visst antall nuller. Gjennomsnittsarbeidet øker eksponentielt med antall nuller som kreves, og arbeidet som er utført kan verifiseres ved å kun gjennomføre en enkelt hashberegning.
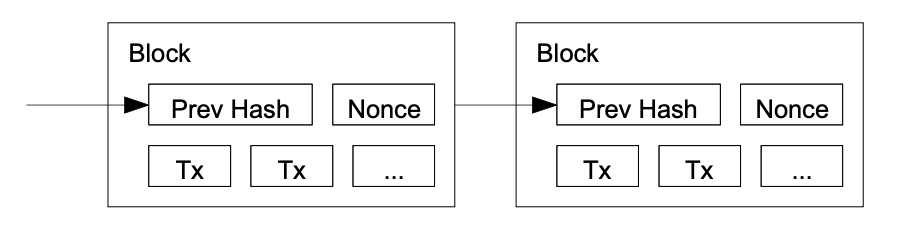
For vårt tidsstemplingsnettverk utfører vi proof-of-work ved å stegvis øke nonce-verdien i blokken til man finner en verdi som gjør at blokkens hashverdi starter med det nødvendige antallet nuller. Når CPU-innsatsen har blitt brukt og oppfyller proof-of-work-kravet, kan ikke blokken endres uten at arbeidet gjøres om igjen. Ettersom etterkommende blokker kobles sammen, vil arbeidet med å endre blokken kreve at man også må gjennomføre arbeidet på nytt for alle de etterkommende blokkene.
Proof-of-work løser også problemet med å bestemme representasjon i flertallsbeslutninger. Hvis flertallet var basert på en stemme for hver IP-adresse, kunne det enkelt ha blitt manipulert av noen som klarte å samle mange IP-adresser. Proof-of-work bygger i hovedsak på prinsippet om en- CPU-en-stemme. Majoritetsbeslutningen er representert av den lengste kjeden, som har mest proof-of-work investert i seg. Hvis en majoritet av CPU-kraft er kontrollert av pålitelige noder, vil den pålitelige kjeden vokse raskest og utkonkurrer andre konkurrerende kjeder. For å modifisere en tidligere blokk, må en angriper omgjøre proof-of-work for blokken og alle blokkene etter den, og ta igjen og overgå arbeidet til de pålitelige nodene. Vi vil senere vise at sannsynligheten for at en tregere angriper tar igjen den pålitelige kjeden reduseres eksponentielt når etterfølgende blokker legges til.
For å kompensere for utviklingen av raskere maskinvare og varierende interesse for drift av noder over tid, blir proof-of-work-vanskelighetsgraden bestemt av et glidende gjennomsnitt som tar sikte på et konstant antall nyskapte blokker per time. Dersom blokker genereres for fort, øker vanskelighetsgraden.
5. Nettverk
Stegene for å drive nettverket er som følger:
- Nye transaksjoner sendes til alle noder.
- Hver node samler nye transaksjoner i en blokk.
- Hver node arbeider for å finne en vanskelig proof-of-work-løsning for sin blokk.
- Når en node finner en proof-of-work-løsning, sender den blokken til alle noder.
- Noder aksepterer bare blokken hvis alle transaksjonene i den er gyldig og ikke allerede utført.
- Noder uttrykker aksept av blokken ved å begynne å arbeide på den neste blokken i kjeden og bruker hashverdien på den aksepterte blokken som forrige hashverdi, som inngår i den nye blokken.
Noder betrakter alltid den lengste kjeden som den sanne og kommer til å fortsette å arbeide med å forlenge den. Hvis to noder sender forskjellige versjoner av blokken samtidig, vil noen noder motta den ene først, mens andre mottar den andre først. I så fall, vil de arbeide på den de mottok først, men lagre den andre grenen i tilfelle den blir større. Disse like blokkene vil bli ødelagt når neste proof-of-work-løsning blir funnet og den ene grenen blir lengre; nodene som arbeidet på den andre grenen vil så bytte til den lengste.
Kringkasting av nye transaksjoner må ikke nødvendigvis nå alle noder. Så lenge de når mange noder, vil de bli inkludert i en blokk innen kort tid. Blokk-kringkasting tåler også tapte meldinger. Hvis en node ikke mottar en blokk, vil noden be om den når den mottar neste blokk og innser at den har gått glipp av en.
6. Insentiv
Ved konvensjon er den første transaksjonen i en blokk en spesiell transaksjon som starter en ny mynt, eid av skaperen av blokken. Dette gir et insentiv for noder til å støtte nettverket, og fungerer som en mekanisme for å allokere nye mynter for sirkulasjon, siden det ikke er noen sentral myndighet til å utstede dem. Den jevne tilstrømningen av en konstant mengde nye mynter kan sammenlignes med gullgravere som bruker ressurser for å sette nytt gull i sirkulasjon. I vårt tilfelle er det CPU-tid og elektrisitet som er ressursene som blir brukt.
Insentivet kan også finansieres av transaksjonsavgifter. Hvis utgangsverdien til en transaksjon er mindre enn inngangsverdien, er differansen en transaksjonsavgift som legges til insentivverdien av blokken som inneholder transaksjonen. Når et forutbestemt antall mynter har blitt satt i sirkulasjon, kan insentivmekanismen gå over til å bare bestå av transaksjonsavgifter og være fullstendig inflasjonsfri.
Insentivmekanismen kan bidra til å oppmuntre noder til å holde seg ærlige. Hvis en grådig angriper er i stand til å samle mer CPU-kraft enn alle ærlige noder, må angriperen velge mellom å bruke kraften til å svindle folk ved å stjele tilbake sine egne betalinger, eller bruke den til å generere nye mynter. Han må finne det mer lønnsomt å følge reglene, regler som belønner ham med flere mynter enn alle andre kombinert, i stedet for å undergrave systemet og validiteten av hans egne verdier.
7. Gjenoppretting av diskplass
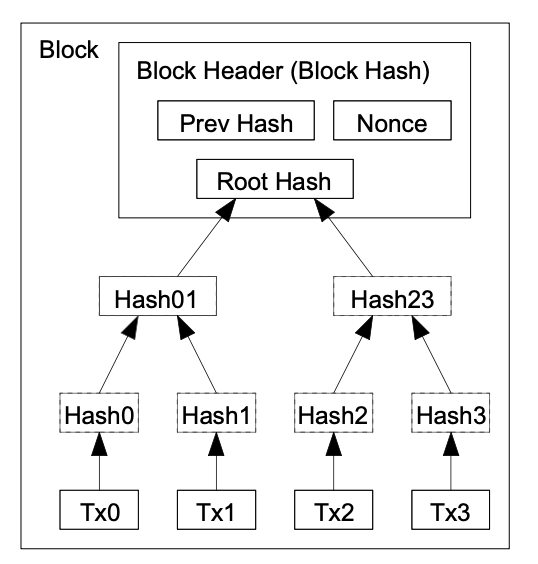
Når den siste transaksjonen i en mynt er begravet under nok blokker, kan de brukte transaksjonene forkastes for å spare diskplass. For å legge til rette for dette uten å ødelegge blokkens hashverdi, hashberegnses transaksjonene i et Merkletre [7] [2] [5], med bare roten inkludert i blokkenes hashverdi. Gamle blokker kan deretter komprimeres gjennom å fjerne grenene på treet. De indre hashverdiene behøver ikke å lagres.
Et blokkhode uten transaksjoner vil være på omtrent 80 bytes. Om vi antar at blokker genereres hvert 10 minutt, 80 bytes * 6 * 24 * 365 = 4,2MB per år. Med datasystemer som vanligvis selges med 2 GB RAM i 2008, og Moores lov som spår at med dagens vekst på 1,2 GB per år, bør lagring ikke være et problem selv om blokkhodene må holdes i minnet.
8. Forenklet betalingsverifisering
Det er mulig å verifisere betalinger uten å drive en full nettverksnode. En bruker behøver bare å oppbevare en kopi av blokkhodet til den lengste proof-of-work-kjeden, som han kan få ved å etterspørre den fra nettverknoder helt til han er overbevist om å han har fått den lengste kjeden, og så skaffe Merkle-grenen som sammenkobler transaksjonen til blokken den er tidsstemplet i. Han kan ikke sjekke transaksjonen selv, men ved å koble den til et plassering i kjeden, han kan se at en nettverksnode har akseptert den, og at blokker lagt til etter den også bekrefter at nettverket har akseptert den.
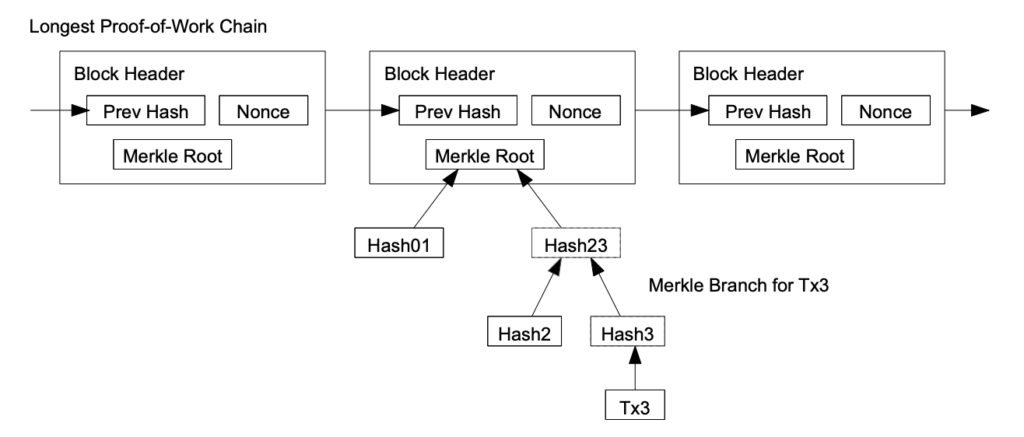
Følgelig er verifikasjonen pålitelig så lenge ærlige noder styrer nettverket, men mer utsatt hvis nettverket overstyres av en angriper. Mens nettverksnoder kan verifisere transaksjoner selv, kan den forenklede metoden bli lurt av en angripers fabrikkerte transaksjoner så lenge angriperen kan fortsette å overstyre nettverket. En strategi for å beskytte mot dette ville vært å akseptere varsler fra nettverksnoder, når de oppdager en ugyldig blokk, som ville fått brukerens programvare til å laste ned hele blokken og varslede transaksjoner for å bekrefte inkonsekvensen. Bedrifter som mottar regelmessige betalinger vil sannsynligvis ønske å drive egne noder for mer uavhengig sikkerhet og raskere verifisering.
9. Kombinering og deling av verdi
Selv om det er mulig å håndter mynter individuelt, ville det vært uhåndterlig å utføre en separat transaksjon for hvert øre som er i en overføring. For å la verdier bli delt og kombinert, må transaksjoner inneholde flere inn- og utgangsverdier. Normalt vil det være en enkelt inngangsverdi fra en større tidligere transaksjon eller flere inngangsverdier som kombinerer mindre beløp, og maksimalt to utgangsverdier: én for betalingen, og én for retur av veksel, dersom noe blir til overs, tilbake til avsenderen.
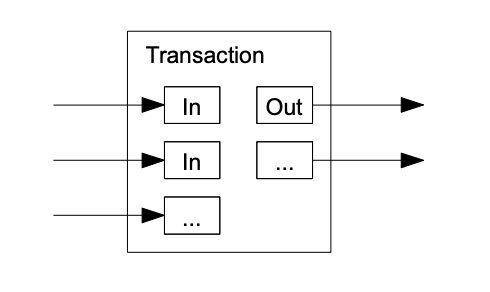
Det burde nevnes at utspenning, hvor en transaksjon er avhengig av flere transaksjoner, og de transaksjonene er avhengig av mange flere, ikke er et problem her. Det finnes aldri behov for å dra ut en fullstendig frittstående kopi av transaksjonshistorikken.
10. Personvern
Den tradisjonelle bankmodellen oppnår personvern ved å begrense tilgangen til informasjon til involverte parter og den betrodde tredjepart. Behovet for å publisere alle transaksjoner utelukker en slik metode, men personvern kan fortsatt opprettholdes ved å bryte strømmen av informasjon på et annet sted: ved å holde offentlige nøkler anonyme. Offentligheten kan se at noen sender et beløp til andre, men uten informasjon som kobler transaksjonene til enkeltindivider. Dette ligner nivået på informasjon utgitt av børser, hvor tid og størrelse for individuelle handler, «båndet», blir offentliggjort, uten å fortelle hvem partene er.
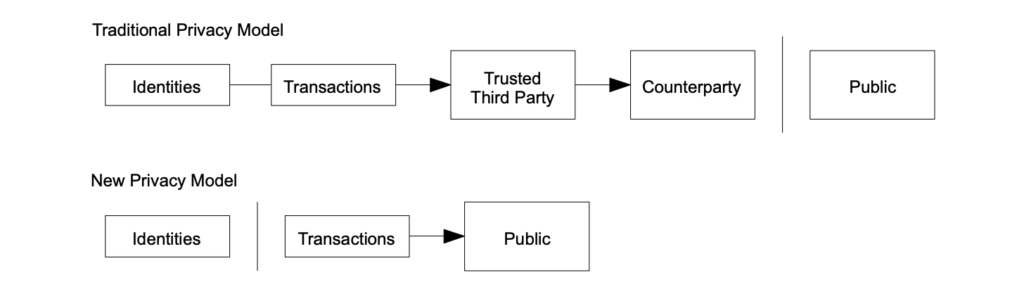
Som en ekstra brannmur bør et nytt nøkkelpar brukes for hver transaksjon for å hindre at de blir koblet til en felles eier. Noen koblinger er fortsatt umulig å unngå med transaksjoner som har flere inngangsverdier, som nødvendigvis avslører at deres inngangsverdier var fra samme eier. Risikoen er at dersom eieren av en nøkkel avsløres, kan koblingen avsløre andre transaksjoner som også tilhørte samme eier.
11. Beregninger
Vi betrakter scenariet hvor en angriper prøver å generere en alternativ kjede raskere enn den sanne kjeden. Selv om dette skulle skje, åpner det ikke systemet for vilkårlige endringer, slik som å skape verdi ut av løse luften, eller ta ut penger som aldri har tilhørt angriperen. Noder kommer ikke til å akseptere en ugyldig transaksjon som betaling, og pålitelige noder vil aldri akseptere en blokk som inneholder dem. En angriper kan bare prøve å endre sine egne transaksjoner for å ta tilbake penger som han allerede har brukt.
Kappløpet mellom den sanne kjeden og en angriperkjede kan karakteriseres som en binomial tilfeldig gange (random walk). Det vellykkede utfallet er at den sanne kjeden blir utvidet med en blokk, øker forspranget med +1, og det mislykkede utfallet er at angriperens kjede blir utvidet med en blokk, noe som reduser forskjellen med -1.
Sannsynligheten for at en angriper tar igjen den sanne kjeden fra et gitt etterskudd, er analogt med Gamblerens konkursproblem. Anta at en gambler med ubegrenset kreditt starter med et underskudd og spiller potensielt et uendelig antall ganger for å forsøke å vinne igjen det tapte. Vi kan beregne sannsynligheten for at han når break-even, eller at angriperen tar igjen den sanne kjeden, som følger [8]:
p = sannsynligheten for at en pålitelige node finner neste blokk
q = sannsynligheten for at angriperen finner neste blokk
qz = sannsynligheten for at angriperen tar igjen fra å ligge z blokker bak
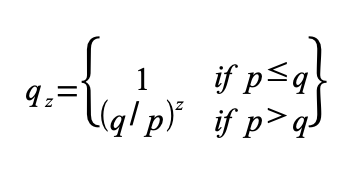
Gitt vår antagelse at p > q faller sannsynligheten eksponentielt når antall blokker angriperen behøver å ta igjen øker. Med oddsen mot ham, hvis han ikke har flaks og lykkes med å komme frem tidlig, blir hans sjanser ubetydelig små når han havner lengre og lengre bak.
Vi vurderer nå hvor lenge mottakeren av en ny transaksjon må vente før det er tilstrekkelig sikkert at avsenderen ikke kan endre transaksjonen. Vi antar at avsenderen er en angriper som ønsker å få mottakeren til å tro at han har betalt ham, og deretter endre det slik at han betaler tilbake til seg selv etter at litt tid har passert. Mottakeren vil bli varslet når det skjer, men senderen håper at det vil være for sent.
Mottakeren genererer et nytt nøkkelpar og gir den offentlige nøkkelen til senderen kort tid etter å ha signert. Dette forhindrer senderen fra å forberede en kjede med blokker på forhånd ved å jobbe kontinuerlig med den til han er heldig nok til å komme langt nok foran, og deretter utføre transaksjonen i det øyeblikket. Når transaksjonen er sendt, vil den uærlige senderen begynne å arbeide i hemmelighet på en parallell kjede som inneholder en alternativ versjon av hans transaksjon.
Mottakeren venter til transaksjonen har blitt lagt til en blokk og z blokker har blitt lagt til etter den. Han vet ikke eksakt hvor stor framgangen til angriperen er, men om man antar at de sanne blokkene brukte den gjennomsnittlige forventede tiden per blokk, vil angriperens potensielle fremgang vil være en Poissonfordeling med forventningsverdi:
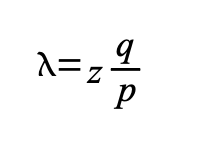
For å finne sannsynligheten for at angriperen fortsatt skal kunne ta igjen kjeden, multipliserer vi Poissonfordelingens tetthetsfunksjon for hvert skritt av fremgang han kunne ha gjort med sannsynligheten for at han kan ta igjen fra det punktet:
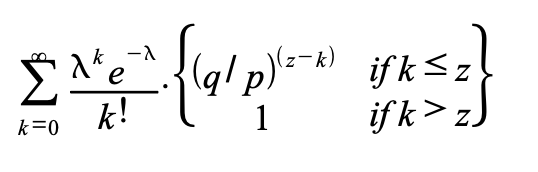
Skriver om for å unngå å summere fordelingens uendelige hale …
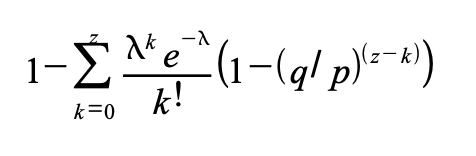
Konvertering til C-kode …
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Når vi tester et antall resultater, ser vi at sannsynligheten faller eksponentielt med z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
Vi løser for P mindre enn 0.1%…
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
12. Konklusjon
Vi har foreslått et system for elektroniske transaksjoner som ikke er avhengig av tillit. Vi begynte med det vanlige rammeverket for mynter laget av digitale signaturer, som gir sterk kontroll over eierskap, men er ufullstendig uten et system for å forhindre dobbeltbetaling. For å løse dette problemet, foreslår vi et P2P-nettverk som ved å bruke proof-of-work skaper en offentlig historikk over transaksjoner, som raskt blir beregningsmessig upraktisk for en angriper å endre hvis ærlige noder styrer brorparten av CPU-kraften. Nettverket er robust i sin ustrukturerte enkelhet. Noder arbeider alle samtidig med begrenset koordinering. De behøver ikke å identifiseres, siden beskjedene ikke blir sendt til en spesiell plass og bare behøver å leveres etter beste evne. Noder kan forlate og koble seg til nettverket som de vil, og akseptere proof-of-work-kjeden som bevis på hva som skjedde mens de var borte De stemmer med deres CPU-kraft, og uttrykker sin godkjenning av gyldige blokker ved å bygge på dem og avslår ugyldige blokker ved å nekte å arbeide med dem. Alle nødvendige regler og insentiver kan håndheves med denne konsensusmekanismen.
Referanser
[1] W. Dai, «b-money,» http://www.weidai.com/bmoney.txt, 1998.
H. Massias, X.S. Avila, and J.-J. Quisquater, «Design of a secure timestamping service with minimal trust requirements,» In 20th Symposium on Information Theory in the Benelux, May 1999.
S. Haber, W.S. Stornetta, «How to time-stamp a digital document,» In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
D. Bayer, S. Haber, W.S. Stornetta, «Improving the efficiency and reliability of digital time-stamping,»In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
S. Haber, W.S. Stornetta, «Secure names for bit-strings,» In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
A. Back, «Hashcash – a denial of service counter-measure,»http://www.hashcash.org/papers/hashcash.pdf, 2002.
R.C. Merkle, «Protocols for public key cryptosystems,» In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
W. Feller, «An introduction to probability theory and its applications,» 1957.
Bitcoin White Paper (PDF Versjon – norsk)
En beskjed fra oversetter
Torbjørn Bull Jenssen sier følgende om oversettelsen:
– Bitcoin representerer en av vår tids største teknologiske gjennombrudd og vil ha enorme effekter på samfunnet vi lever i. Det er derfor viktig at informasjon er bredest mulig tilgjengelig og for mange vil det være enklere å lese på norsk enn engelsk. I tillegg er norsk et flott språk som jeg mener det er viktig å holde i hevd gjennom bruk.
Hva betyr dette dokumentet for deg?
For meg er bitcoin-dokumentet et eksempel på at teknologi kan drive samfunnsendringer nedenfra og opp; at en ide på en e-postliste kan vokse frem organisk, én konvertert skeptiker av gangen, og gjennom evolusjon finne en form som er relevant for stadig flere.
Enda viktigere; hva betyr bitcoin sitt white paper for verden og samfunnet forøvrig?
Bitcoin sitt white paper representerer en av tidenes sommerfugleffekter. Et dokument delt på en e-postliste for kryptografiinteresserte, som nå, 11 år senere, danner grunnlaget for satsinger fra verdens største selskap og stater.
Dette skaper store økonomisk muligheter for de som er villige til å gripe dem.
Men kanskje viktigere så bærer bitcoin fortsatt med seg et løfte om uavhengighet og likebehandling; en frihet for individet til å utveksle verdier med hvem de vil, uansett hvem de er og hvor de måtte befinne seg.
Hva er det mest fascinerende perspektivet med teksten?
Noe av det mest fascinerende er kanskje hvor kort og enkelt det er. Man behøver hverken være en ekspert på kryptografi eller datamaskiner for å skjønne det.
Det er ikke en lettlest skjønnlitteratur, men bruker man litt tid på å sette seg inn i det, er det forståelig for de fleste.
Hvilke problemer dukket opp når dere oversatte dokumentet?
Den største utfordringen var å finne gode formuleringer og ord for fagbegreper som ikke nødvendigvis finnes på norsk.
I tillegg er den orginale “white paper” utgaven ingen god oversettelse der – ikke alltid like godt språklig, selv om det er enkelt skrevet. Det er for eksempel en del steder hvor argumentasjonen er noe springende, som var ekstra utfordrende å oversette.




